Hoy
nos toca una nueva tarea de matemáticas. Como vimos a Fibonacci y su
famosa secuencia, vamos a seguir trabajando las sucesiones o series.
Acordaos de que hay un trabajo mínimo para hacer y entregar y un
“nivel PRO” voluntario pero muy interesante.
¡Vamos
a ello!
- 1º
y 2º de primaria
AQUÍ
TE PONEMOS EL VÍDEO QUE CUENTA LA TAREA:
Si
os queréis descargar el cuaderno de actividades, aquí está.
La
secuencia de Fibonacci relacionaba los números con la naturaleza.
¿Os
acordáis de hacer series? Si, ¿verdad? Ya os propusimos algunas la
semana anterior. Pero ahora vamos a ver muchas posibilidades.
En
un principio nos centraremos en series de sumar. Hay que rellenar los
recuadros sumando al número que hay o habéis escrito en el recuadro
anterior, el número que hay sobre la flecha. Las que tienen flechita
son las más sencillas. Ejemplo:
1.-
Ahora vienen las que tenéis que hacer. Primero una facilita, que
tiene constante la suma:
2.-
Cuidado con la siguiente: estad atentos pues los números que se
suman, cambian.
3.-
Subimos un nivel y quitamos la flecha. Primero hay que deducir qué
número se suma con los que ya están escritos, y luego seguir la
serie:
4.-
También nos las pueden encargar restando. En este caso deduciremos
el número que hay que ir quitando en cada caso:
5.-
Como en el circo: “¡Más difícil todavía! Si nos dan los números
en el centro de la serie, para completar un lado tendremos que restar
y para el otro, sumar. No digo a la izquierda o derecha porque todo
puede ser, tal como podréis comprobar ahora:
¡Vaya,
vaya! Estas dos últimas ya podrían ser nivel PRO. Pero bueno,
también se pueden hacer series con símbolos o dibujos:
7.-
Esta con fichas de dominó, tendréis que mirar cómo son y rellenar
las azules, termina con el seis doble:

______________________________________________________
Nivel
PRO:
Vídeo
que explica el nivel PRO. Aquí lo tenéis:
Las
series de números más difíciles no tienen tan siquiera un número
fijo que suma o resta. Hay que deducirlo a partir de los anteriores.
1.-
La secuencia de Fibonacci es un buen ejemplo, pues para escribir el
siguiente número había que sumar los dos anteriores. Como salen
sumas llevando las podéis hacer juntando lentejas, trocitos de
papel, lapiceros,… Prohibido copiarla.
¡Enhorabuena!
Habéis construido la secuencia de Fibonacci, unos números muy
curiosos. Veamos la historia de este matemático en este vídeo que
es la reseña del libro “Fibonacci, el soñador de números”.
Una
vida marcada por las matemáticas. ¿Os ha gustado?
Y
para terminar este nivel PRO concluiremos con otras dos series de las
difíciles.
2.-
Son difíciles porque las sumas van variando y no nos lo ponen con
una flechita. ¡Animo!:
3.-
Esta tiene su bonito dibujo, sigue el camino:
Pon
en marcha tu creatividad: esta serie va con lentejas, pero puedes
usar arroz, garbanzos, pegatinas pequeñitas, trocitos de papel,…
4.-
Os proponemos que la terminéis tan larga como queráis y con la
forma y orientación que os dé la gana, pero respetando y que sean
visibles los grupos con los números 1, 3, 5,… Luego, usando
vuestra imaginación, tendréis que componer un dibujo en el que los
objetos usados formen parte del mismo:
Aquí
termina la tarea. Esperamos que de tanto trabajar con las series os
hayáis sentido Fibonacci por un día y que seáis un poco más
matemáticos que al principio.
Como
siempre, copiáis las actividades, las hacéis en el cuaderno y, una
vez terminadas, las mandáis a vuestros tutores de la forma
acostumbrada.
- 3º y 4º de primaria
El
lunes anterior conocimos la secuencia de Fibonacci, que relacionaba
los números con la naturaleza. Habéis entregado muy buenas
realizaciones. ¡Os felicitamos!
Vamos
a continuar con más sucesiones como la de Fibonacci. ¿Os acordáis
de hacer series? Si, ¿verdad? Ahora vamos a ver muchas
posibilidades. En este vídeo te orientamos en la faena:
Si
os queréis descargar el cuaderno de actividades, aquí está.
En
un principio nos centraremos en series de sumar.
1.-
Tenéis que rellenar los recuadros sumando al número del recuadro
anterior el término que debéis deducir de los números que ya están
escritos:
2.-
En esta se suma 9, prueba sumando primero 10 y luego resta 1:
3.-
A veces, las series se calculan restando:
4.-
Y otras veces nos colocan los números en el centro, por lo que hay
que sumar a un lado y restar al otro.
Todas
estas series se calculan sumando o restando un número que es el
mismo siempre. Pero no siempre es así.
5.-
Subimos un nivel y el número que se suma o resta ha de deducirse de
los anteriores siendo variable, como pasaba en la secuencia de
Fibonacci, que es la primera que os proponemos:
6.-
No es la única, aquí tenéis otras dos de sumando variable:
La
primera secuencia que habéis hecho en el ejercicio 6, sirvió para
ilustrar la leyenda del inventor del ajedrez. ¿La conocéis? Aquí
está:
7.-
También se pueden hacer secuencias con imágenes: esta con fichas de
dominó, tendréis que mirar cómo son y rellenar las azules. Pista:
termina con el seis doble:
______________________________________________________
Nivel
PRO:
En
el vídeo tenéis la presentación del nivel PRO:
Como
en el circo: “¡Más difícil todavía! También se pueden hacer
multiplicando o dividiendo.
1.-
A continuación tenéis varias posibilidades:
Esta
dos últimas series que acabáis de completar son muy queridas por
los ordenadores. ¿Os suena la palabra “bit”?
2.-
Aquí tenéis otras que se resuelven multiplicando:
Poned
en marcha vuestra creatividad: esta serie está construida con
lentejas, pero puedes usar arroz, garbanzos, pegatinas pequeñitas,
trocitos de papel,…
3.-
Os proponemos que la terminéis tan larga como queráis y con la
forma y orientación que os dé la gana, pero respetando y que sean
visibles los grupos con los números 1, 3, 5,… Luego, usando
vuestra imaginación, tendréis que componer un dibujo en el que los
objetos usados formen parte del mismo:
Aquí
termina la tarea. Esperamos que de tanto trabajar con las series os
hayáis sentido Fibonacci por un día y que seáis un poco más
matemáticos que al principio.
Como
siempre, copiáis las actividades, las hacéis en el cuaderno y, una
vez terminadas, las mandáis a vuestros tutores de la forma
acostumbrada.
- 5º y 6º de primaria
El
lunes anterior conocimos la secuencia de Fibonacci, que relacionaba
los números con la naturaleza. Habéis entregado muy buenas
realizaciones. ¡Recibid nuestro reconocimiento!
Vamos
a continuar con más sucesiones como la de Fibonacci. ¿Os acordáis
de hacer series? Si, ¿verdad? Ahora vamos a ver muchas
posibilidades. En el siguiente vídeo te proponemos la tarea:
Si
os queréis descargar el cuaderno de actividades, aquí está.
En
un principio nos centraremos en las series más fáciles, las de
sumar.
1.-
Tenéis que rellenar los recuadros sumando al número del recuadro
anterior el término que hay que deducir de los números que ya están
escritos:
1 3 5 ___ ___ ___ ___ ___ ___
3 6 9 ___ ___ ___ ___ ___ ___
2.-
En esta se suma 9, usa como truco sumar 10 y luego restar 1:
5 14 ___ ___ ___ ___ ___ ___ ___
3.-
Y en esta se suma 19, piensa si puedes usar un truco parecido:
2 21 ___ ___ ___ ___ ___ ___ ___
4.-
A veces, las series se calculan restando:
45 40 35 ___ ___ ___ ___ ___ ___
5.-
Y otras veces nos colocan los números en el centro, por lo que hay
que sumar a un lado y restar al otro.
___ ___ ___ 12 15 18 ___ ___ ___
___ ___ 26 22 18 ___ ___ ___ ___
Todas
estas series que habéis hecho, cuando se suma o resta un número
fijo, las estudiaréis en el instituto. Se llaman “progresiones
aritméticas”.
Subimos
un nivel y el número que se suma o resta ha de deducirse de los
anteriores.
6.-
Así pasaba en la secuencia de Fibonacci, que es la primera que os
proponemos:
1 1 2 3 5 ___ ___ ___ ___ ___
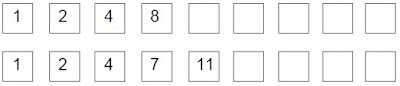
7.-
A continuación tenéis otras dos. Pensad cómo se forman:
1 2 4 8 ___ ___ ___ ___ ___
1 2 4 7 11 ___ ___ ___ ___ ___
La
primera secuencia que habéis hecho en el ejercicio 7, sirvió para
ilustrar la leyenda del inventor del ajedrez. ¿La conocéis? Aquí
está:
Como
en el circo: “¡Más difícil todavía! También se pueden hacer
multiplicando, que es lo que hizo el inventor del ajedrez.
8.-
Aquí tenéis varias posibilidades:
3 6 12 ___ ___ ___ ___ ___
1 5 25 ___ ___ ____ ____ _____
1 10 100 ____ _____ _____ _______
___ ___ 8 16 32 ___ ___ ___ ___
Esta
última secuencia que acabáis de completar es muy apreciada por los
ordenadores. ¿Os suena la palabra “bit”?
______________________________________________________
Nivel
PRO:
En
el vídeo tenéis la presentación del nivel PRO:
1.-
Comenzamos el nivel PRO sin decir cómo se calculan. Hay que hacer
pruebas:
___ 3 9 27 ___ ___ ____ ____
___ 10 ___ ___ 80 ____ ____ 640
¿Pensáis
que no se pueden hacer dividiendo?. Por supuesto.
2.-
Como muestra, basta un botón. Esta serie va de dividir:
1024 512 256 ___ ___ ___ ___ ___
Estas
que se calculan multiplicando o dividiendo por un número fijo se
conocen en matemáticas como “progresiones
geométricas”
Ahora
tendréis que poner lo mejor de vosotros porque os vamos a pedir
sumar los términos de una serie.
3.-
Empecemos con el ejemplo de una secuencia numérica en la que sumamos
4:
3 7 11 15 19 23 27 31 35 39
Sumar
los diez números es engorroso, escribid el resultado: _____
Ahora
probad a sumar el primero y el último: 3
+ 39 = ______
El
segundo y el penúltimo: 7
+ 35 = _____
El
tercero y el antepenúltimo: 11
+ 31 = _____
Y
así sucesivamente: _______, ________.
¿Qué
casualidad, no? Teníamos 10 números y nos han salido,
evidentemente, cinco pares que suman lo mismo. Si multiplicamos la
suma de un par por cinco, que son las parejas de números que nos han
salido ¡nos sale la suma total de los números de la serie! Por
supuesto es más cortito resolver la pregunta de esta forma.
4.-
¿Seríais capaces de calcular la suma de una secuencia si os decimos
que el primer número es un 1, el último 39, y hay 20 números en la
secuencia?
Comprobadlo:
sólo hay que añadir que el número que sumamos es el 2. Así podéis
construir la serie para sumar todos los números.
Mucho
más cómodo hacer una suma y una multiplicación, ¿no?
5.-
¿Seríais capaces de saber qué hacer para calcular la suma si no
todos los números se pueden emparejar? Ejemplo:
1 3 5 7 9 11 13
Os
avisamos que esto es ya nivel PROPRO.
Aquí
termina la tarea. Esperamos que de tanto trabajar las series os
hayáis sentido Fibonacci por un día y que seáis un poco más
matemáticos que al principio.
Como
siempre, copiáis las actividades, las hacéis en el cuaderno y, una
vez terminadas, las mandáis a vuestros tutores de la forma
acostumbrada.














No hay comentarios:
Publicar un comentario